Renters rente kan sende din aktieindkomst på

Hvorfor er renters rente vigtigt for dig?

Du kan tjene grotesk mange penge på dine aktier, hvis du forstår renters rente.

Den berømte investor Warren Buffet udtalte, at hans enorme formue kom fra: '... en kombination af, at leve i America, heldige gener ... og renters rente.'

Albert Einstein tilskrives citatet: "Rentes renter er verdens 8. vidunder. Den, der forstår det, tjener godt på det; den der ikke forstår det, betaler for det."

Hvis du allerede er rigere end Warren Buffet og/eller klogere end Albert Einstein, så behøver du ikke læse videre.

Reklame

Hvem vil du helst være?

En, der tjener mange, nemme penge på at forstå renters rente? Eller,
En af dem, der betaler for det?

Læs med her, og så er du er allerede godt på vej til at komme i den første kategori. Der kommer en smule matematik. Men bare rolig. Alle udregningerne er lavet for dig - og forklaret med letforståelige grafer.

Matematikken er desværre nødvendig, da renters rente er det klassiske eksempel på en såkaldt eksponential funktion.

Formlen for beregning af renters rente

Formlen for renters rente ser således ud:

$Slutbeløb = Startbeløb * \lparen 1 + rente\rparen^{antal~år}$

Første eksempel: 5% rente over 20 år

Lad os antage, at du har kr. 10.000 på en bankkonto, og du får 5% i rente hvert år. Du hæver aldrig penge på kontoen. Du sætter heller ikke flere penge ind. Efter første år, får du tilskrevet renter. Efter andet år, får du ekstra renter, da du nu også får renter, af det første års renter.

Hvordan ser det ud efter 20 år?

Udfyld formlen således:
$Slutbeløb = 10.000 * \lparen 1 + 0.05\rparen^{20}$

Det giver denne graf:

So f.cking what tænker du måske?

De 5% kræver mere end 20 år, før effekten slår igennem. Vi booster processen ved at sætte renten op.

Forskellen på 5 og 10% rente over 20 år

Se nu, hvad der sker, bare ved at vi sætter renten op til 10%. Alt andet er det samme. Nu ser formlen således ud:

$Slutbeløb = 10.000 * \lparen 1 + 0.10\rparen^{20}$

Vi begynder allerede at ane, at der begynder at ske noget efter 10 - 12 år.

Forskellen ved 15% rente over 20 år

Vi giver renten endnu et nøk mere opad til 15%. Alt andet er det samme. Formlen bliver så:

$Slutbeløb = 10.000 * \lparen 1 + 0.15\rparen^{20}$

20% rente over 20 år

Vi giver renten endnu en tak opad til 20%. Alt andet er det samme. Formlen bliver så:

$Slutbeløb = 10.000 * \lparen 1 + 0.20\rparen^{20}$

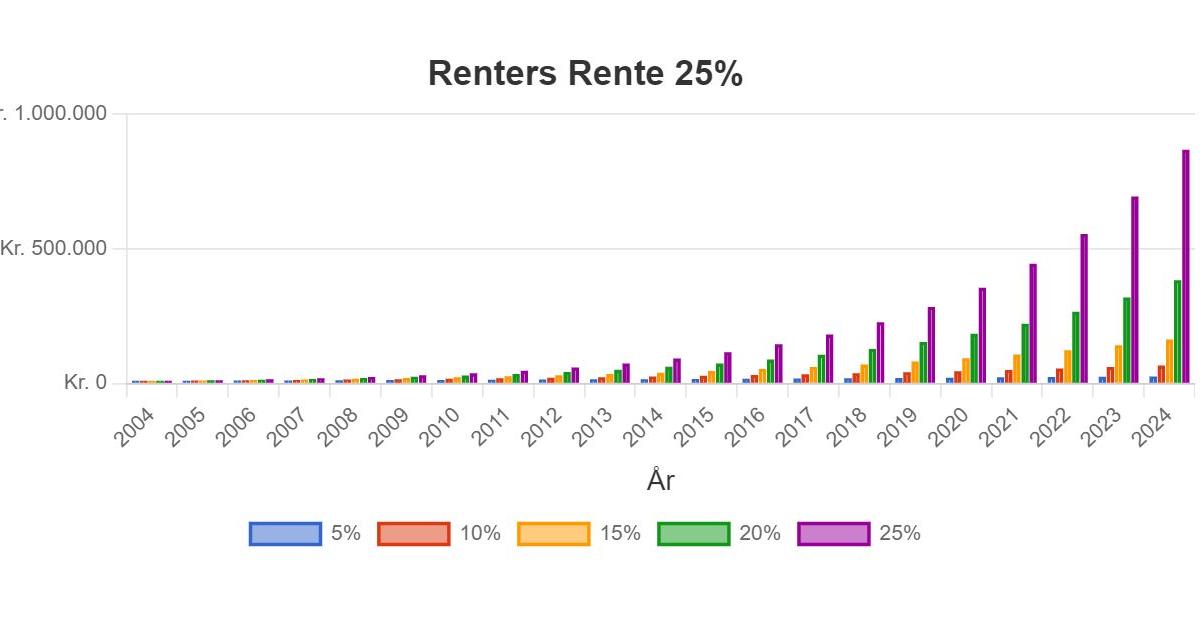
25% rente over 20 år

Renten sættes nu til 25%. Alt andet er det samme. Formlen bliver:

$Slutbeløb = 10.000 * \lparen 1 + 0.25\rparen^{20}$

Hvad er renters rente?

Renters rente er så de renter du får, af alle de renter, der er tilskrevet din konto, alle de forudgående år.

Begår du også denne fejl med renters rente?

De fleste, der lærer om renters rente, regner kun 2 eller 3 år frem i tiden, og så stopper de der. Beløbet stiger jo kun en lille smule, så det virker som spild af tid, at regne videre.

Og det er en kæmpe fejl, der kan koste dig dyrt.

Forstå eksponential funktioner.

Tegner man funktionens udvikling over tid, vil den vokse meget langsomt i starten. Men, pludselig går udviklingen endog meget stærkt.

Nærmest som en lille snebold, der ruller ned ad en bjergside. I starten ser det ikke ud af meget, men den bliver til en altødelæggende lavine længere nede.

Forestil dig, hvor rig du ville blive, hvis det samme skete med dine penge!

HVORDAN WARREN BUFFET BLEV MILLIARDÆR MED RENTERS RENTE